
Synergické sekvence
Stránka není dokončena - zatím sbírám materiály :-)
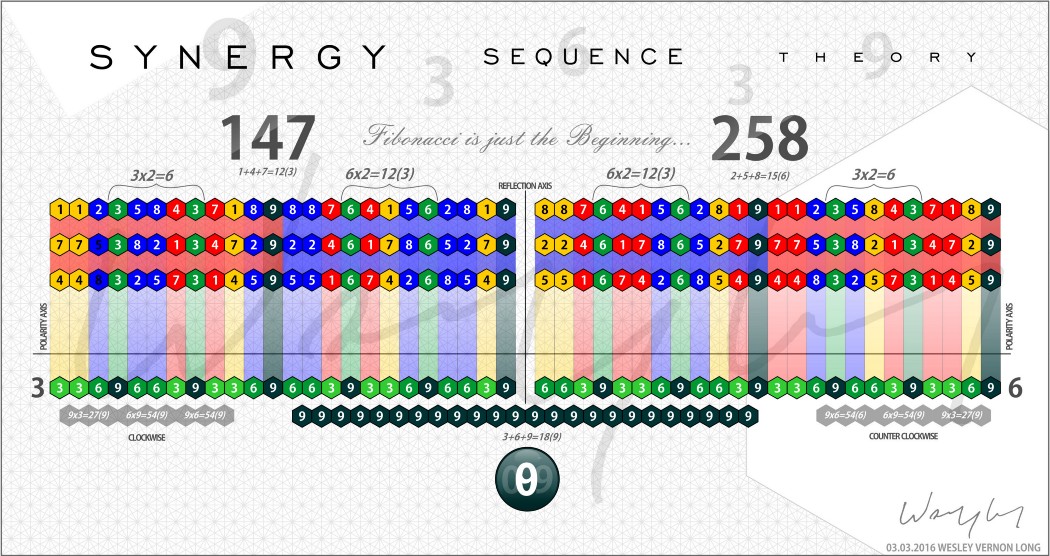
Sekvenční mapa je zajímavý způsob, jak sledovat vzájemné vztahy a chování.
Bez pochyb je polarita a odraz.
Od této chvíle bude skupina 147 označována jako G3, skupina 258 se stane G6 a skupina 369 bude G9.
Tyto skupiny se chovají velmi odlišně od každého čišr ale úzce souvisí současně. Jakákoli dvě čísla G3 se budou rovnat číslu G6, zatímco jakákoli dvě čísla G6 se budou rovnat číslu G3. Jedno číslo z G3 a jedno z G6 se bude rovnat číslu G9. Toto chování je identické s individuálním chováním čísla G9 (3,6,9). To znamená, že čísla dědí vlastnosti a chování jejich skupiny čísel.
Další analýza mapy odhalí ještě zajímavější informace. Každá sekvence začínající Fibonacciho sekvencí kromě čísel G9 obsahuje 18 polarizovaných pozic. Červenou si můžete představit jako severní/pozitivní a modrou jako jižní/negativní.
Když o tom takhle přemýšlíme, co s tím můžeme dělat?
Právě se mi stalo, že kolem mě kopala hromada neodymových magnetů, a tak jsem se rozhodl otestovat čísla. Ve skutečnosti by to byl konečný způsob, jak zjistit, zda to, co vidím, je skutečné.
Okamžitě, když jsem si začal hrát s magnety, jsem viděl a cítil, jak matematika v této sekvenční mapě ožívá. Byl jsem přesvědčen, že je to skutečné, ale stále to nebylo důkazem ničeho. Je všeobecně známo, že protiklady se přitahují zejména pomocí magnetů, tak co?
Při pohledu na odpovědi na mapu sekvence jsem pozoroval 2 její velmi důležité aspekty. Čísla stejné skupiny se navzájem odrážela! Také jsem si všiml, čemu říkám klíčové snímky. Konkrétně sekvence vytvářejí 6 klíčových rámců. Počet bodů nalezených v přírodním světě příliš často na to, aby to byla náhoda, šestiúhelník. Něco tu bylo a potřeboval jsem to dokázat.
Rozhodl jsem se zkonstruovat několik solidních testů pro ladění a pochopení toho, co jsem viděl, praktickým a fyzickým způsobem. Vyřízl jsem 6 trojúhelníků a do každého bodu trojúhelníků vyvrtal 3 otvory. Začal jsem Fibonacciho sekvencí a namapoval magnety na póly nalezené v každé z 18 pozic s výjimkou skupiny G9, která se používá k označení bodů odrazu.
Do této chvíle bylo hodně z toho, co jsem našel, docela přesvědčivé, ale teď jsem držel v ruce fyzickou ukázku toho, co jsem viděl na mapě. Držel by šestiúhelník pohromadě? Objevilo se opravdu bizarní a úžasné chování. V závislosti na tom, jak je nakonfigurujete, může sever přitahovat sever a totéž platí pro jih. A co víc, pokud budete přesně sledovat 18 pozic, vytvoříte šestiúhelník, který drží pohromadě. Ve skutečnosti je to jeden z toho, co se zdá být jen 2 způsoby, jak bude držet pohromadě.
Narazil jsem do králičí nory a věřím, že je velká šance, že jsem učinil významný objev. Ten, který by mohl změnit způsob, jakým lidé přemýšlejí o číslech. Je ironií, že tuto králičí díru založil Fibonacci, který objevil Fibonacciho sekvenci při pokusu vypočítat rychlost, jakou se králíci za rok rozmnožovali. Nesnažil jsem se vyřešit vesmír ani příliš zatěžovat numerologií nebo duchovní stránkou čísel, jako to dělá příliš mnoho. Jednoduše jsem pracoval na nějaké modulační matematice pro program, na kterém jsem pracoval.
I decid ed používat 3,6,9 jako základ pro své odlišení, protože Nikola Tesla citát o 3,6,9, že klíč k vesmíru, tak proč ne? Vypadá to jako zajímavé výchozí místo, že? Rychle jsem objevil nekonečně se opakující vzorec. Po několika vyhledáváních na Googlu a na YouTube jsem zjistil, že nejsem jediný, kdo to zkoumal.
Existuje mnoho odkazů a videí, které hovoří o významu 3,6,9. Vortexová matematika je nejzajímavější, i když ji mnozí neberou vážně. Začal to Marko Rodin a dělá mnoho výstředních tvrzení o vortexové matematice, která ji spojuje s Bohem a spiritualitou s "vyššími" úrovněmi. Mluví o vyléčení všech nemocí, volné energie a ukončení nedostatku potravin v kostce, kterou prohlašuje, že vírová matematika může vyřešit každý problém, který svět má. Jsou i další. Po vyčerpávajícím zkoumání čehokoli souvisejícího s matematikou, vortexovou matematikou a numerologií je velkou výhodou, že lidé, kteří to zkoumají, hledají Boha. Minimálně ti, kteří o tom blogují nebo to dávají na youtube.
Najdou jakýkoli malý vzor a informace o třešních, které by odpovídaly jejich ideologii. Není to tak, že by to nebyly dobré teorie, jakmile jim porozumíte. Bohužel zkreslení veškeré matematiky se stále vrací do toho, co si myslím, že je země fantazie. Nechápejte mě špatně, nemám nic proti jakémukoli náboženství nebo systému víry, faktem je, že by to mohlo velmi dobře podpořit jejich názory a posílit jejich víru. Mohou to být dokonce mimozemšťané.
Lidé se od začátku snaží vysvětlit svět pomocí čísel. Učinili tak s hvězdami, náboženstvím a podivuhodnými strukturami, které charakterizují důležitost matematiky a způsob, jakým by měla být interpretována.
Nedostal jsem se do tohoto hledání Boha a dokonce ani poté, co jsem objevil to, co by mohlo být pro některé Boží lidi důkazem. Nechám to na zvážení ostatním. Pustil jsem se do toho a hledal jsem praktické využití pro 3,6,9 číslic. Hledání tvrdých faktů a věcí, které mohu použít, a nic mě nemohlo připravit na to, co jsem se chystal odhalit.
V matematice existuje nespočet záhad. Kde se to vzalo? Byl objeven nebo vynalezen? Jaký je konec Pi? Jak se "zlatý poměr" nebo Fibonacciho posloupnost v přírodním světě objevují tak často? Problém je, že jedna věc nefunguje na všechno a stále existuje mnoho tajemství, která je třeba vyřešit. Nenašel jsem odpovědi na všechno, ale jsem si docela jistý, že to, co jsem našel, je obrovská stopa a povede to k lepšímu pochopení matematického a přírodního světa.
DŮLEŽITÁ POZNÁMKA: Vše, co se chystáte vidět, lze vypočítat a ověřit. Neber to za slovo. Nic jsem nepřikrášloval ani nefotil, aby to vyhovovalo jakékoli agendě. Je to čistá matematika. Ve skutečnosti je to pravděpodobně matematika v té nejčistší formě. Zkuste to sami a uvidíte, k jakým závěrům dojdete. I když se mýlím nebo jsem úplně mimo, budete mít jeden pekelný trik, který můžete ukázat na večírcích nebo na hodinách matematiky pro lidi, kteří milují čísla.
Digital Root
Začněme s digitálním rootem. Pokud slyšíte poprvé termín digitální kořen, zde je citát z Wikipedie.
" Digitální kořen (také opakovaný digitální součet) nezáporného celého čísla je (jedna číslice) hodnota získaná iteračním procesem sčítání číslic, při každé iteraci pomocí výsledku z předchozí iterace k výpočtu číselné sumy. Proces pokračuje, dokud není dosaženo jednociferného čísla. "
Abychom si ujasnili, pokud máme číslo 25, digitální root bude výsledkem sčítání 2 a 5 k celkovému 7. Takže 25 má digitální root 7. Snadné! Mějte to na paměti.
Fibonacci
1,1,2,3,5,8,13,21,34,55,89...
Velkou záhadou je, jak lze tuto sekvenci nalézt v tolika věcech od rostlin a včelstev po zvířata a přírodní systémy. Existuje také mnoho odkazů na starověký svět, který to chápe a do všeho zabudovává "Zlatý poměr". Ve skutečnosti to vědecká komunita celosvětově přijala a je to hlavní součást jakéhokoli matematického kurzu nebo osnov. Matematici a vědci si dnes lámou hlavu nad tím, jak může fungovat s tolika věcmi, ale ne se vším. Věřím, že zde můžeme konečně začít hledat odpověď.
Fibonacci bude ještě zajímavější, když použijete digitální root
1, 1,2, 3, 4, 5, 8, 13 (4), 21 (3), 34 (7), 55 (1), 89 (8),
1,1,2,3,5,8,4,3,7,1,8,9,8,8,7,6,4,1,5,6,2,8,1,9
Jakmile dosáhnete 24. výsledku, sekvence se bude opakovat a opakovat do nekonečna. To bezpochyby přispívá k vábení Fibonacciho.
Rozhodl jsem se zkusit experiment. Stejnou metodou k vytvoření Fibonacciho posloupnosti jsem vytvořil sekvence pro čísla 1-9.
Potom jsem všechny výsledky redukoval na jejich digitální kořen. Objevily se podobné nekonečně se opakující vzory pro každou z 9 číslic.
112358437189887641562819
224617865279775382134729
336966393369663933696639
448325731459551674268549
551674268549448325731459
663933696639336966393369
775382134729224617865279
887641562819112358437189
999999999999999999999999
Okamžitě jsem si všiml, že 3,6 a 9 jsou extrémně odlišné od ostatních. 3 a 6 skutečně překlápějí nebo mají nějakou polaritu. Skutečně interagují s 9 nebo s ním souvisejí. Sekvence 9 vrací nekonečno 9 s. Jedna teorie ve Vortex Math se týká rodinných číselných skupin. Seskupují 1,4,7 jako jednu skupinu, 2,5,8 jako druhou a 3,6,9 jako konečnou skupinu.
Důvod, proč to uvádějí, je prezentován velmi matoucím a neurčitým způsobem, občas si říkáte, jestli tomu rozumí. Aby toho nebylo málo, znečišťují své prezentace teologií a příliš se zamotávají do toho, co to všechno znamená, protože se to týká nějakého druhu božství nebo řešení všeho. Nemůžete jen tak skočit dopředu a hádat odpověď.
Zde je několik chladných tvrdých faktů o rodinných číselných skupinách. Bezpochyby jsem dokázal, že existují způsobem, který lze otestovat a dokázat. Pomocí Fibonacciho metody k vytvoření mých sekvencí jsem si všiml velmi zajímavého vzoru. Pomocí oddělovače 9 jsem rozdělil 24místný opakující se vzor na dva 12místné obrazce a uvědomil jsem si, že druhý vzor 12 byl přesně stejný jako první vzor 12 jiné sekvence a to platilo pro všech 9 sekvencí.
Způsob, jakým se vzory shodují, se ve skutečnosti dělí 1-9 na 3 skupiny (1,4,7) (2,5,8) a (3,6,9). Doslova vytváří polaritu mezi čísly a skupinami čísel.
Obrázky v horní části stránky tyto skupiny a toto chování vizualizují, ale teprve začínáme.
V tomto okamžiku jsme vytvořili dva zajímavé důkazy. 1. Fibonacci je jedna posloupnost 9. Pokud se Fibonacciho posloupnost v životě tolik shoduje, ale ne se všemi, bylo by logické, že odpovědi by mohly být v dalších 8 posloupnostech. 2. Použití těchto nových sekvencí, které následují po Fibonacciho metodě, poskytuje dokonalý důkaz o existenci číselných skupin a polárních párů. Jak jsem řekl, právě začínáme! Více o těchto sekvencích a co znamenají dále v tomto příspěvku. Nyní se zaměřme na 369.
"Zlatý" standard Když
zkoumáme, jak se tyto sekvence mohou odehrávat v reálném světě, začneme se dostávat do "zlatého poměru" a dalších Fibonacciho.
Když se podíváme na "Zlatý trojúhelník" a "Zlatý obdélník", první věc, kterou bych chtěl zdůraznit, je, že byly označeny jako "Zlaté", protože se zdálo, že nabízejí nejvíce esteticky příjemný poměr. To je hrozný důvod. Použití těchto "zlatých" teorií přináší hodně polopřesné výsledky, ale zase ne všechno. Ani blízko.
Od 16 let jsem byl grafickým designérem a dělal jsem rozvržení školních novin. Nyní ve 39 letech mám 23 let zkušeností s extrémní přesností práce s tvary, měřítky a poměry, jak zjistíte. Zkoušel jsem různé tvary a velikosti s vyčerpávající iterací. Jistě všechny spirály a vzory vypadají skvěle, ale pár věcí mi stále vadilo. Ne vždy to funguje a aby bylo dosaženo stejné struktury jako v přírodě, chtělo by to nějaké doladění. Vědci to připisují změnám ve "zlatém poměru" a nepolapitelnosti Pi.
Než budu pokračovat, rád bych řekl, že matematika je úžasná. Bez ohledu na to, jak tomu říkáme, jsou čísla velmi reálná a probíhající výpočty, které vedou náš svět a vesmír, jsou skutečné. Největší technologie na Zemi je matematika, protože nás přivedla k tomuto bodu. Všechno v moderním světě je díky matematice.
Synergický trojúhelník a poměry
Pochopil jsem chování číselných skupin, polárních čísel a odlišných vzorců ze skupiny 3,6,9, spolu s původním Tesla citátem, který mě v tom začal, rozhodl jsem se zkusit pracovat s trojúhelníkem s úhly 30 (3), 60 (6) a 90 (6). Jsem si jistý, že architekti a inženýři a zejména vývojáři her si musí být vědomi toho, jak všestranný může být tento trojúhelník a tyto úhly. Počet tvarů a vzorů, které můžete pomocí tohoto trojúhelníku vytvořit, je neomezený. A co víc, tento specifický trojúhelník se může donekonečna zvětšovat a udržovat všechny proporce a poměry. .Velmi to funguje jako bubliny. Ano, řekl jsem bubliny! Pokud jste nikdy neviděli nebo neviděli nic o vědě o bublinách, doporučuji to zkontrolovat. Opravdu úžasné věci. Bubliny se obvykle spojují pod úhlem 120 (3) stupňů a vždy se optimalizují pro povrchovou plochu. Pomocí Synergy Triangle můžete vytvořit mřížku, která prakticky odpovídá chování bublin. Rozhodl jsem se blíže podívat, proč. Co je na těchto úhlech tak zvláštního?
Vytvořil jsem to, čemu říkám Synergický kompas, který mapuje různé orientace trojúhelníku a všech odpovídajících úhlů na 30, 60 a 90. Kompas jako Fibonacciho metoda vytvořil smyčkový vzor 963, jak je znázorněno níže. Králičí nora pokračuje...
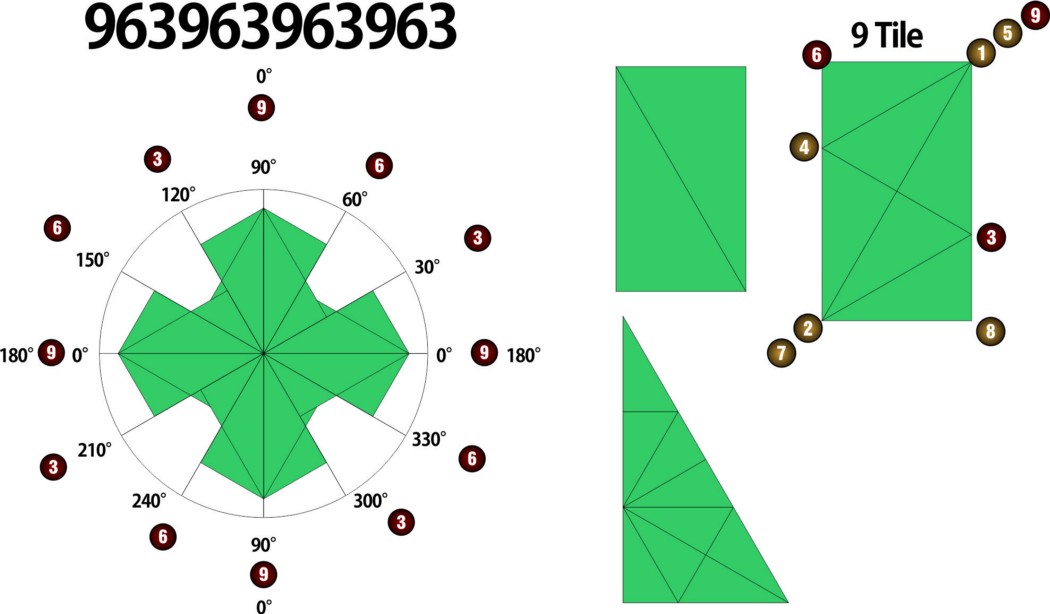
Dobře, vážně, tato 369 se objevuje ve všem. Co s tím mám dělat? Co to znamená v praxi? Podívejme se, co je na tomto trojúhelníku a těchto číslech tak zvláštního. Zapomínáme na Fibonacciho, Phi, Pi, "zlaté poměry", Pythagorase a všechny jejich psy, začněme od začátku.
Pokusme se vysvětlit svět v 369 a jejich odpovídajících poměrech a úhlech.
Určitě se mi líbí mnoho, napsal jsem článek o planetě Saturn, když jsem byl v 6. ročníku. Vždy to byla moje oblíbená planeta. Je jedinečný v mnoha ohledech a přesto, že je zakrnělý Jupiterem, je to "hvězda" naší sluneční soustavy, samozřejmě vedle našeho slunce. Můžete předpokládat, že je to kvůli prstenům a nebudete se úplně mýlit, ale budete se mýlit. To může nebo nemusí být známá teorie nebo ne. Nejsem si jistý, ale věřím, že Saturn je nejmladší planetou naší sluneční soustavy. Množství materiálu a úlomků, které krouží kolem prstenců a měsíců, by mohlo znamenat zrození pevné planety jako Země před našimi očima. Extrémně jedinečný rys Saturnova severního pólu v jasném tvaru šestiúhelníku by mohl být rysem, který by každá planeta mohla mít během svého vývoje.
Po celém "živém" světě zde na Zemi jsou šestiúhelníky. Saturn by mohl být šiška! Semeno planety.
Nakreslil jsem kruh o průměru 3 cm, následoval další na 6 cm a uhodli jste, další na 9 cm. Poté jsem kruhy vycentroval
dokonale a překryl je na spodní pohled na Saturn. Výsledkem bylo upadnutí čelisti. Jistě, mnoho seriózních vědců může být k této metodě skeptických, ale já jsem to neudělal přesně. Poměry byly dokonale zmapovány, jak je vidět níže, dokonce až k samotnému vnějšímu prstenci. Možná to není 100% přesné, ale myslím, že je bezpečné říci, že je to hit. Rychle se začalo hromadit 369 zásahů, takže jsem to potřeboval rozdělit na praktické poměry.
Řekněme, že máte Synergy Triangle otočený na 90 a obličej s nejkratší šířkou je zarovnán ke dnu. Představte si levý dolní roh jako výchozí bod cesty z vašeho GPS. Pro jednotky použijeme kroky. Uděláte jeden krok vpřed, doleva otočíte o 60 stupňů, uděláte další 2 kroky, otočíte doleva o 30 stupňů a pak půjdete rovně, odkud jste začali. Tato délka není na 0,866 kroku úplně krokem. Abyste se tam dostali, budete muset mít částečný krok 0,116 kroku, neboli 23,46% délku kroku. Tento trojúhelník také tvoří dokonalý šestiúhelník, který lze neomezeně obkládat. To by vysvětlovalo, proč včely staví úly tak, jak to dělají, ne proto, že by to bylo nejlepší využití prostoru, ale proto, že je to pro ně doslova snadný vzorec s využitím vlastních těl jako referencí. V jejich případě by pravidlem byly 2 kroky, otočte o 120 stupňů a opakujte, dokud se nevrátíte na začátek. To také odpovídá tomu, jak bubliny fungují, spojují se při 120 stupních, což odpovídá 30 nebo (3). 3 jednoduché kroky 1- 2- otočte 30 a opakujte. Zdá se, že šestiúhelníky jsou jádrem přírody s nesčetnými příklady. Zahrnuji některé, ale v každém případě si najděte svůj vlastní a zkuste to sami.

Všimněte si, že každý řádek na borovicovém kuželu je přesně o 23,46% větší než předchozí a že digitální kořen celého desetinného čísla je 1. Přesně to, čím jsme začínali. Mám pocit, že by to mohl být klíč k pochopení toho, jak desetinná místa skutečně fungují. Myslím, že "zlatý poměr" je zlatý řez, protože první desetinné číslo je 6. Myslím, že jakýkoli poměr, který má digitální kořen 3,6 nebo 9, lze v přírodě najít stejně často.
Mám více výzkumu a práce s poměry pro 369, ale myslím, že jsem jasně ukázal, jak mohou souviset s přírodním světem, takže prozatím pojďme dál. Brzy zveřejním více o těchto 3 poměrech.
A co sekvence synergie?
Fibonacci se tedy odráží v přírodě, 369 se odráží v přírodě. Co teď? Máme k prozkoumání dalších 7 sad sekvencí. Naštěstí prozatím nemusíme přistupovat ke každé sekvenci jeden po druhém, můžeme to ladit dohromady.
Moje první myšlenka byla mřížka a začít hledat nové vzory. Nejprve jsem vytvořil čtvercovou mřížku a zapojil se do sekvencí, abych viděl, jaký druh matice vytvoří a jak se bude chovat. Na první pohled je to jako bláznivé desetinné místo, které pokračuje navždy. Některé části matice fungovaly, některé ne a začínalo to být velmi matoucí. Rozhodl jsem se zkusit šestiúhelník, protože je pro tuto teorii důležitý a posun každého řádku by usnadnil sledování a ladění. Špatně! Stále to bylo matoucí. Některé části fungovaly, některé ne, ale bylo zřejmé, že v těchto sekvencích byly skutečné vizuální vzory a že vše bylo zrcadleno.
Nastavil jsem rychlý animovaný gif na kole přes všechna zvýrazněná čísla. (Jak je vidět níže) Nastavil jsem rychlosti animace na ... počkejte na to ... 3,6,9.

To je zajímavé ... Vypadá to, že se něco otáčí nebo teče po skutečné síti !!! ??? Je to skutečné? Fibonacciho sekvence, když je spárována s podobnými sekvencemi generovanými jinými čísly stejnou metodou jako Fibonacci, jen tak namaluje zatracenou mřížku plynulým spinny? Vypadni odsud! Matematika je šílená!
Odbočil jsem.
Jistě, skutečnost, že to máme v mřížce, částečně vysvětluje tvar, ale ne do této míry. Vážně, to je docela zajímavé, zkusme rozebrat, na co se díváme. Po studiu a "česání" nad každým z rámců jsem si vizuálně všiml stejného efektu zrcadlení a polarizace, jaký jsem viděl v číslech, a začal jsem kombinovat vzory podle skupin čísel a polárních párů. Myslel jsem, že to vytvoří nějaký druh vlny nebo funky počítačového vzoru, a to nebylo úplně špatné, ale to, co se ukázalo v mém pohledu, bylo šílené.
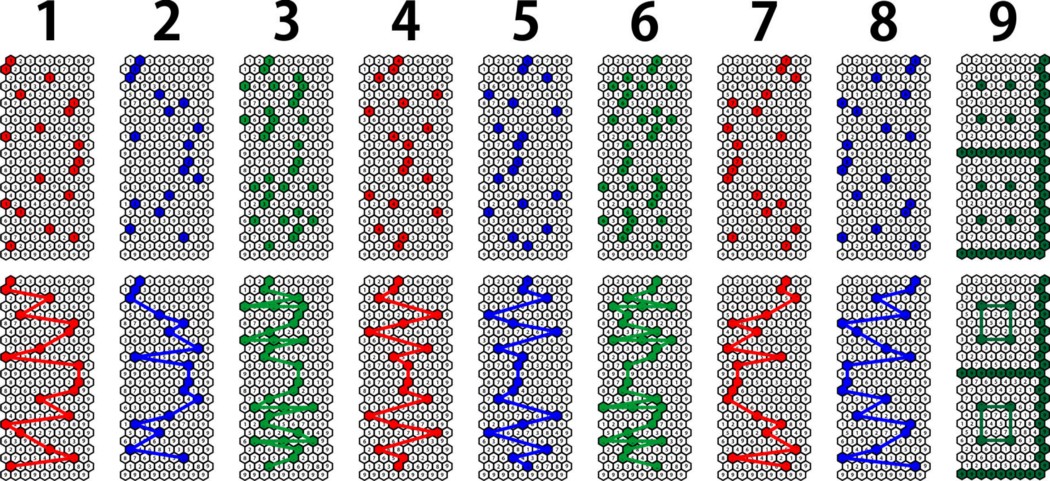
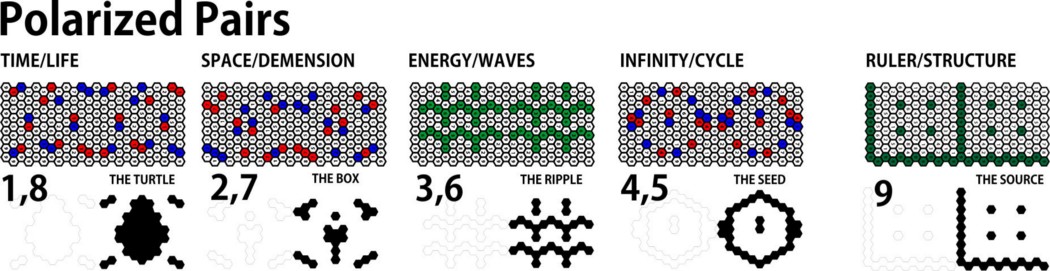

Toto je přímá zpráva z matematiky, z čísel a vodítka, co jsou čísla, vlastně co všechno je. Neříkám tak či onak, jestli existuje bůh, nebo jestli jsou to mimozemšťané, o tom se dá znovu uvažovat a debatovat v průběhu času jako o všem ostatním. Myslím, že je docela těžké hádat, co by tyto symboly mohly znamenat, ale o tom musíte diskutovat. Mým cílem je jednoduše tyto informace dostat ven a zůstat ve všem logický, objektivní a kritický. Jen fakta, jen čísla, prostě MATKA! Pokud si myslíte, že jsem něco zkreslil, zkuste to sami. Jsem si jistý, že budete mít přesně stejný výsledek.
Synergická matice a mnoho dalšího, co přijde...

Nedávno jsem objevil klíč k matici a jak to funguje, ale není to snadné vysvětlit v současné podobě a ještě těžší je v tomto formátu představit. Pracuji na programu, který také zveřejním a který umožní lidem experimentovat a hrát si s matrixem online, aby zjistili, co dalšího dokáže kromě toho, co jsem našel.
Právě jsem poškrábal povrch toho, co jsem objevil. Jsem doslova přes 100 stránek hluboko do výzkumu a výpočtů, které jsem dělal, a pracuji na tom, abych to všechno destiloval a dostal online, aby to lidé mohli studovat spolu s dalšími animacemi a způsoby, jak to všechno modelovat a rozbít, aby to plně pochopili. Rovněž zvu a vítám jakoukoli spolupráci, proto mě prosím kontaktujte na zkráceně Wesley.V.Long@SynergySequenceTheory.com nebo wes@synergysequencetheory.com .